Jump Search

×

Input the Desired Array

* Size Should be in Range (5 - 300)
* Enter space seperated integers ,Total of above size.
* For better Visibility each interger is of range (21 - 550).
* Enter a sorted array, jump seach only works on an sorted array

* Only for searching algorithms
* Enter only one value

Introduction: Jump Search Algorithm is a relatively new algorithm for searching an element in a sorted array. The fundamental idea behind this searching technique is to search fewer number of elements compared to linear search algorithm (which scans every element in the array to check if it matches with the element being searched or not). This can be done by skipping some fixed number of array elements or jumping ahead by fixed number of steps in every iteration.

WORKING OF JUMP SEARCH

Step 1: Let us trace the above algorithm using an example: Consider the following inputs:
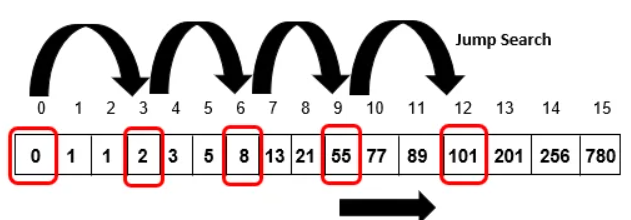
A[] = {0, 1, 1, 2, 3, 5, 8, 13, 21, 55, 77, 89, 101, 201, 256, 780} item = 77
m = √n = 4 (Block Size)

Step 2: Compare A[0] with item. Since A[0] != item and A[0] less than item, skip to the next block

Step 3: Compare A[3] with item. Since A[3] != itemand A[3] less than item, skip to the next block

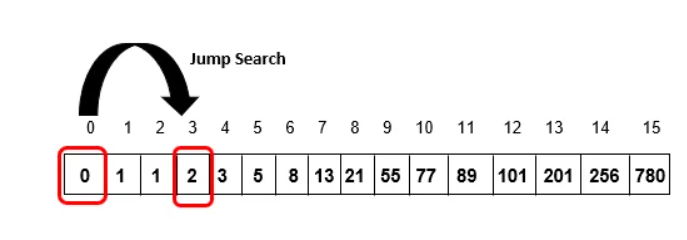
Step 4: Compare A[6] with item. Since A[6] != itemand A[6] less than item, skip to the next block

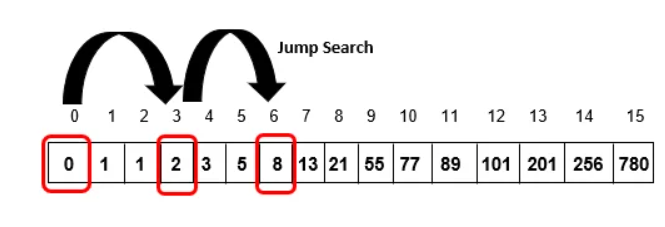
Step 5: Compare A[9] with item. Since A[9] != itemand A[9]less than item, skip to the next block

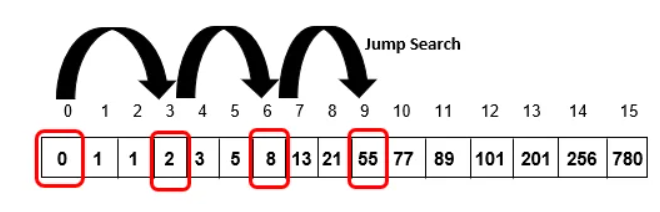
Step 6: Compare A[12] with item. Since A[12] != item and A[12] > item, skip to A[9] (beginning of the current block) and perform a linear search.

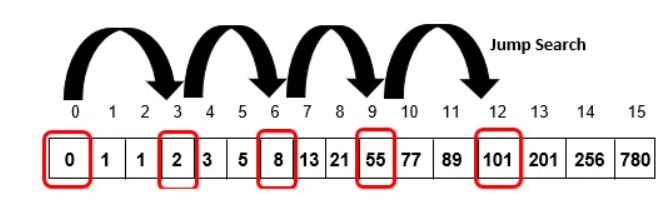
Step 7: Compare A[9] with item. Since A[9] != item, scan the next element
Compare A[10] with item. Since A[10] == item, index 10 is printed as the valid location and the algorithm will terminate


We conclude that the target value 31 is stored at location 5. Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.