Exponential Search

×

Input the Desired Array

* Size Should be in Range (5 - 300)
* Enter space seperated integers ,Total of above size.
* For better Visibility each interger is of range (21 - 550).
* Enter a sorted array,Exponential seach only works on an sorted array

* Only for searching algorithms
* Enter only one value

Introduction: We utilize the same produced integers ( powers of 2 ) to hop indexes in an array and come closer to the index of the key.
In this technique, eventually, we depend on Binary Search for searching, but before that, we determine a range in which the element we want to search could be present.

WORKING OF EXPONENTIAL SEARCH

There are basically two phases involved in conducting an exponential search:-
1.Finding the range in which the key could sit
2.Applying binary search in this range
a) Start with value i=1
b) Check for a condition I less than n and Array[i] less than or equal to key, where n is the number of items in the array and key is the element being sought
c) Increment value of I in powers of 2, that is, i=i*2
d) Keep on incrementing the value of I until the condition is met
e) Apply binary on the range i/2 to the end of Array - binarySearch(Array, i/2, min(i,n-1))

Step 1:Consider the array:- 1 3 5 7 9 11 13 15 17 19
Element to search: 19

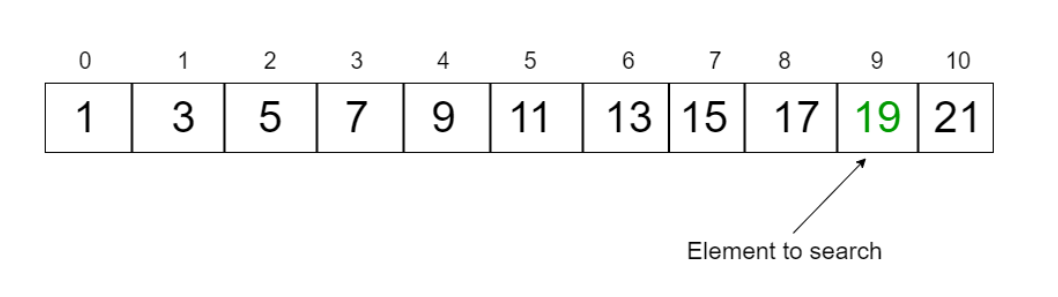
Step 2:We will start by comparing Array[0] element to the key, which in our instance will yield false.
I will be initialized to 1
Now we will carry on incrementing the value of I until it is less than or equal to the key.

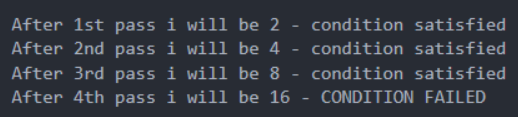
Step 3:Note that the value of I is now 16, and the index 16 is out of range in this instance, thus to recover the previous value of I we will divide it by 2, then run a binary search using the index as low as i/2.
Now we call the binary search technique.
binarySearch(Array, i/2, min(i, n-1), key)

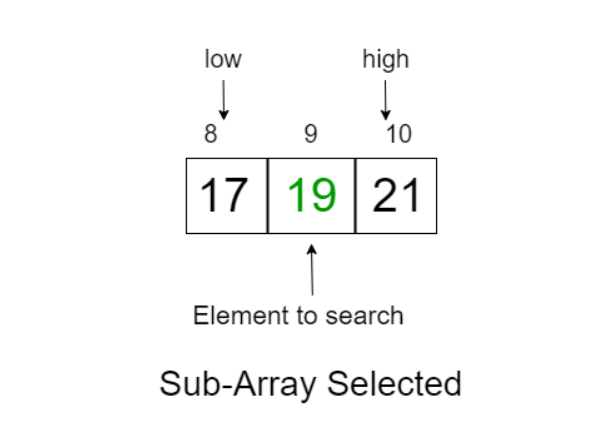
Step 4:Finding the required element
Array[9]=19, which is the required element.